Np Complete Vs Np Hardclevelandmultifiles

Posted on by



  • Design and Analysis of Algorithms
  • Nurse practitioner programs are often part of a master's degree program and prepare graduates to perform advanced levels of medical care. Those who earn a Master of Science in Nursing may focus on.
  • NP-Complete- The group of problems which are both in NP and NP-hard are known as NP-Complete problem. Now suppose we have a NP-Complete problem R and it is reducible to Q then Q is at least as hard as R and since R is an NP-hard problem. Therefore Q will also be at least NP-hard, it may be NP-complete also.
  • The problem in NP-Hard cannot be solved in polynomial time, until P = NP. If a problem is proved to be NPC, there is no need to waste time on trying to find an efficient algorithm for it. Instead, we can focus on design approximation algorithm. NP-Complete Problems. Following are some NP-Complete problems, for which no polynomial time algorithm.
  • In computational complexity theory, a problem is NP-complete when:. A nondeterministic Turing machine can solve it in polynomial-time.; A deterministic Turing machine can solve it in large time complexity classes (e.g., EXPTIME, as is the case with brute force search algorithms) and can verify its solutions in polynomial time.
  • Basics of Algorithms

This discussion is deliberately fuzzy, since it is supposed to be addressed to a child as per the question. They have years to learn the right details. To keep things simple, let's just talk about problems with "yes/no" answers.

  • Design Strategies
  • Graph Theory
  • Heap Algorithms
  • Sorting Methods
  • Complexity Theory
  • DAA Useful Resources
  • Selected Reading

A problem is in the class NPC if it is in NP and is as hard as any problem in NP. A problem is NP-hard if all problems in NP are polynomial time reducible to it, even though it may not be in NP itself.

If a polynomial time algorithm exists for any of these problems, all problems in NP would be polynomial time solvable. These problems are called NP-complete. The phenomenon of NP-completeness is important for both theoretical and practical reasons.

Definition of NP-Completeness

A language B is NP-complete if it satisfies two conditions

  • B is in NP

  • Every A in NP is polynomial time reducible to B.

If a language satisfies the second property, but not necessarily the first one, the language B is known as NP-Hard. Informally, a search problem B is NP-Hard if there exists some NP-Complete problem A that Turing reduces to B.

The problem in NP-Hard cannot be solved in polynomial time, until P = NP. If a problem is proved to be NPC, there is no need to waste time on trying to find an efficient algorithm for it. Instead, we can focus on design approximation algorithm.

Np Complete Vs Np Hardclevelandmultifiles Exam

NP-Complete Problems

Following are some NP-Complete problems, for which no polynomial time algorithm is known.

  • Determining whether a graph has a Hamiltonian cycle
  • Determining whether a Boolean formula is satisfiable, etc.

NP-Hard Problems

The following problems are NP-Hard

  • The circuit-satisfiability problem
  • Set Cover
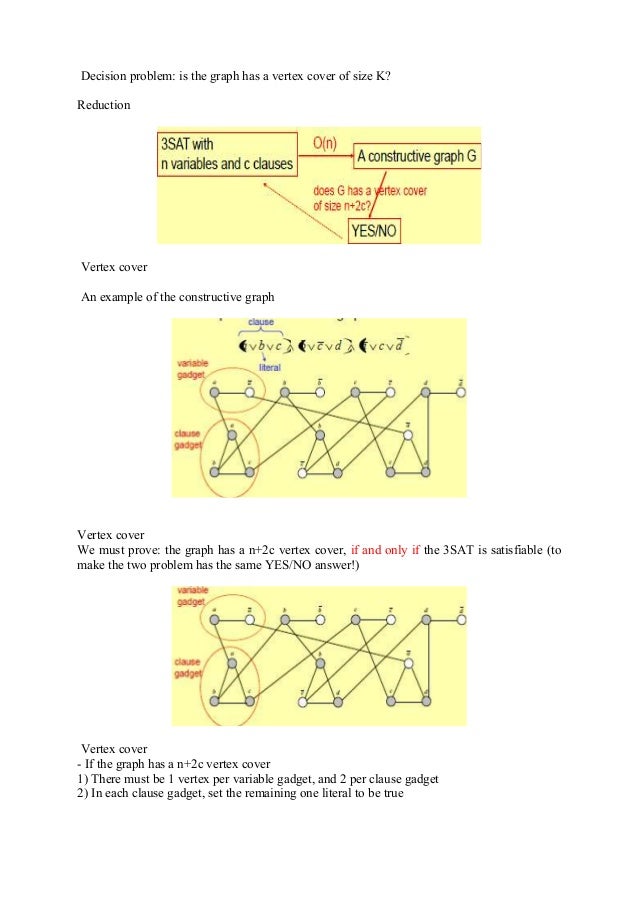
  • Vertex Cover
  • Travelling Salesman Problem

In this context, now we will discuss TSP is NP-Complete

TSP is NP-Complete

The traveling salesman problem consists of a salesman and a set of cities. The salesman has to visit each one of the cities starting from a certain one and returning to the same city. The challenge of the problem is that the traveling salesman wants to minimize the total length of the trip

Proof

To prove TSP is NP-Complete, first we have to prove that TSP belongs to NP. In TSP, we find a tour and check that the tour contains each vertex once. Then the total cost of the edges of the tour is calculated. Finally, we check if the cost is minimum. This can be completed in polynomial time. Thus TSP belongs to NP.

Np Complete Vs Np Hardclevelandmultifiles Scope

Secondly, we have to prove that TSP is NP-hard. To prove this, one way is to show that Hamiltonian cycle ≤p TSP (as we know that the Hamiltonian cycle problem is NPcomplete).

Np complete vs np hardclevelandmultifiles pharmacologyComplete

Assume G = (V, E) to be an instance of Hamiltonian cycle.

Complete

Hence, an instance of TSP is constructed. We create the complete graph G' = (V, E'), where

$$E^{'}=lbrace(i, j)colon i, j in V ::and:ineq j$$

Thus, the cost function is defined as follows − Ce fata ai download for mac free.

Np Complete Vs Np Hardclevelandmultifiles Nursing

$$t(i,j)=begin{cases}0 & if: (i, j): in E1 & otherwiseend{cases}$$

Np Complete Vs Np Hardclevelandmultifiles Test

Now, suppose that a Hamiltonian cycle h exists in G. It is clear that the cost of each edge in h is 0 in G' as each edge belongs to E. Therefore, h has a cost of 0 in G'. Thus, if graph G has a Hamiltonian cycle, then graph G' has a tour of 0 cost.

Conversely, we assume that G' has a tour h' of cost at most 0. The cost of edges in E' are 0 and 1 by definition. Hence, each edge must have a cost of 0 as the cost of h' is 0. We therefore conclude that h' contains only edges in E.

Np Complete Vs Np Hardclevelandmultifiles Pharmacology

We have thus proven that G has a Hamiltonian cycle, if and only if G' has a tour of cost at most 0. TSP is NP-complete.